Przedstawię tu dość ścisłe, mające oparcie w fizyce, uzasadnienie powstawania pływów oraz ich częstości. Zastosuję dopuszczalne uproszczenia wynikające z faktu, że rozmiary Ziemi są znacznie mniejsze od odległości między Ziemią a Księżycem. Pominę też wpływ Słońca jako mniej istotny czynnik pływowy. Pozwala to stworzyć model bardziej klarowny dla zrozumienia istoty rzeczy.
W rzeczywistości, według Keplera, środki obu ciał poruszają się po elipsach, a środek masy układu - barycentrum, znajduje się w ich ogniskach, pomiędzy Ziemią a Księżycem. Leży on w odległości e (patrz rysunek), ok. ¾ promienia Ziemi od jej środka czyli ok. 4700 km. Założymy dla uproszczenia, że ruch tych ciał odbywa się po okręgach współśrodkowych w barycentrum B. Odległość r między środkami mas Ziemi i Księżyca wynosi ok. 400 000 km. Rozważymy układ sił działających na masę próbną m, wynikający z towarzystwa Księżyca. Siły grawitacji Ziemi i siły odśrodkowe wynikające z jej dobowego ruchu wirowego, w dowolnym punkcie Ziemi są stałe, co do wartości i kierunku, w układzie odniesienia związanym z Ziemią - nie powodują zatem zmian ukształtowania jej powierzchni płynnej. Grawitacja czyni planetę kulą, a ruch wirowy rozpłaszcza ją nieco na biegunach w elipsoidę obrotową (z grubsza). Darujmy więc sobie dobowy ruch wirowy, gdyż on nie powoduje pływów.
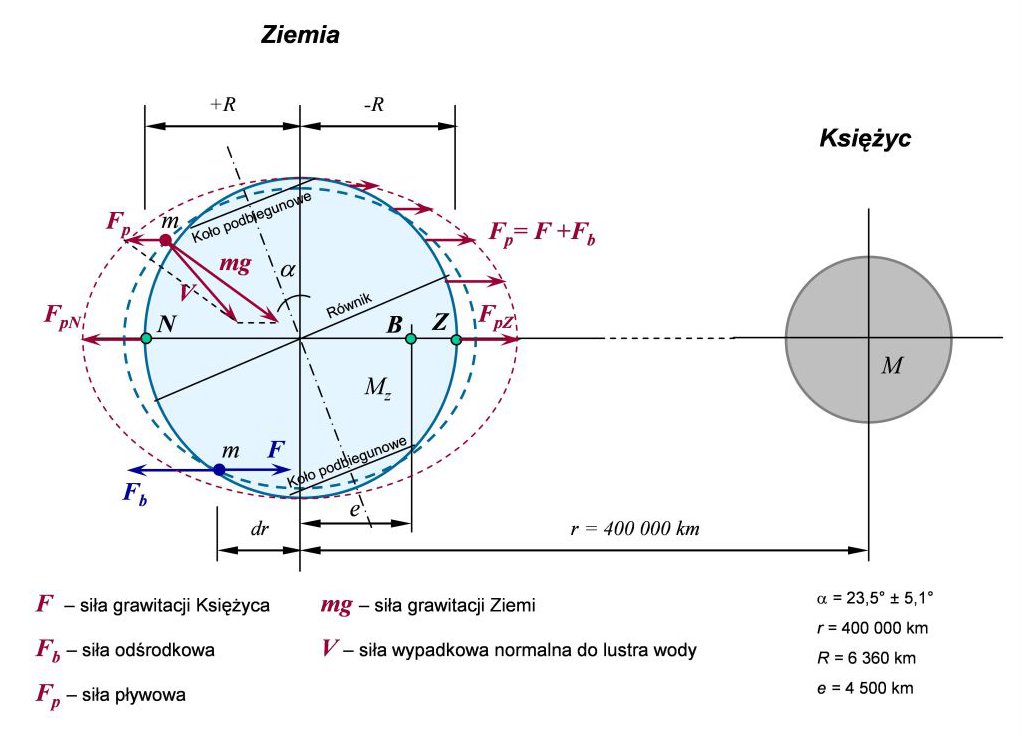
Na rysunku pokazano Ziemię i Księżyc widoczne z płaszczyzny orbity, która jest prostopadła do płaszczyzny kartki, z osią ziemską leżącą w płaszczyźnie kartki. Nachylenie osi nie ma znaczenia dla rozkładu sił pływowych odniesionych do osi Ziemia-Księżyc czyli linii oddziaływań ciał, ale punkty na Ziemi biegnące w ruchu dobowym po równoleżnikach, prostopadłych do osi, będą poruszały się w polu zmiennych sił pływowych.
Dla masy m umieszczonej w odległości r od Księżyca, siła grawitacji działająca na nią ze strony Księżyca jest funkcją jednej zmiennej - odległości r:
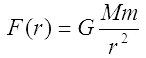
Różniczka zupełna tej funkcji określa zmianę (przyrost lub spadek) wartości siły grawitacji działającej na masę m dla położeń różniących się od r o wartość dr, nieskończenie małą w stosunku do r: dr << r
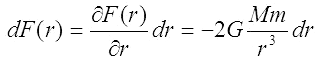
dr jest składową odległości elementu m od środka Ziemi, na kierunek Ziemia-Księżyc. Korzystamy tu z założenia, że Księżyc jest odległy, kierunek działania sił grawitacji między elementem m a Księżycem jest prawie równoległy do linii łączącej środki obu ciał niebieskich, czyli kierunku działania wypadkowych sił grawitacji wiążących te ciała.
Całkowita siła grawitacji, działająca ze strony Księżyca na element masy m, wynosi zatem:
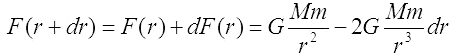
Jednocześnie punkt oddalony o dr od środka Ziemi znajduje się w odległości e+dr od osi rotacji Ziemi wokół wspólnego środka ciężkości B układu ciał niebieskich, jeśli element masy leży w płaszczyźnie prostopadłej do orbity zawierającej promień wodzący r. Siła odśrodkowa działająca na element m ma wartość:
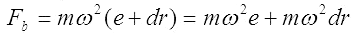
ω jest częstością krążenia (prędkość kątowa)
Siła pływowa jest wektorową sumą oddziaływania grawitacyjnego Księżyca i siły odśrodkowej wynikającej z obiegu Ziemi wokół punktu B. Ponieważ jednak założyliśmy, że odległość do Księżyca jest znacznie większa od promienia Ziemi, więc w przybliżeniu wektory tych sił leżą wzdłuż prostej łączącej środki obu ciał niebieskich. Suma wektorowa sprowadza się więc do sumy algebraicznej. W każdym razie w dwóch punktach N i Z, które rozważymy później, jest to ścisłe.
Siła pływowa ma zatem wartość:
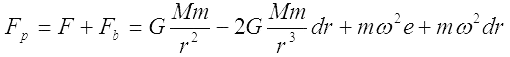
grupując otrzymujemy:
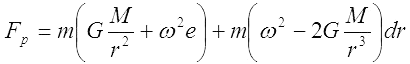
Zauważmy, że pierwszy składnik tego równania nie jest zależny od dr i wyraża siły grawitacji oraz dośrodkową (lub odśrodkową) dla masy umieszczonej w środku Ziemi.
Zwróćmy uwagę, że dla Ziemi obowiązuje, wynikająca z drugiej zasady dynamiki, równość siły grawitacji i siły bezwładności (odśrodkowej):
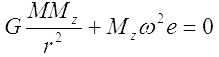
dzieląc obustronnie przez Mz otrzymujemy:
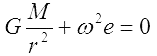
co podstawiamy do wzoru na siłę pływową Fp.
Otrzymujemy zatem:
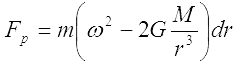
Widać więc, że rozwiązanie jest symetryczne względem płaszczyzny normalnej do osi Ziemia-Księżyc i przechodzącej przez środek Ziemi. Jest to płaszczyzna zerowych sił pływowych. Dla odległości dr dodatnich, po stronie dalszej od Księżyca otrzymujemy dodatnią wypadkową siłę od wpływu Księżyca, skierowaną od niego. Dla dr ujemnych - siłę równą co do wartości lecz z przeciwnym znakiem, więc skierowaną w stronę Księżyca. Widać, że siły pływowe będą rozciągały płynną oceaniczną otoczkę Ziemi w elipsoidę o osi długiej leżącej wzdłuż linii Ziemia-Księżyc. Co więcej, po obu stronach tej płaszczyzny pływy oceaniczne (swobodne) będą podobne.
Ze złożenia sił grawitacji ziemskiej mg i siły pływowej Fp (na rysunku w lewej górnej ćwiartce Ziemi) wynika, że wypadkowa V jest odchylona. Jest ona normalna (prostopadła) do powierzchni wody, gdyż ta jest powierzchnią w przybliżeniu ekwipotencjalną. Ruch pływowy wody nieco to zaburza.
Sprawdźmy, jakie są siły pływowe w dwóch przeciwległych punktach Z i N. Wyznaczamy je przechodząc z dr do wartości skończonych równych promieniowi Ziemi R << r:
-
w punkcie Z (Księżyc w zenicie) oddalonym od środka Ziemi o dr = -R
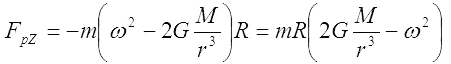
-
w punkcie N (Księżyc w nadirze) oddalonym od środka Ziemi o dr = R
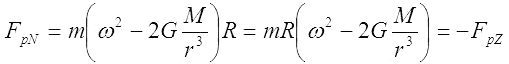
Z tych zależności widać, że po stronie Księżyca siła grawitacji przeważa nad siłą odśrodkową „kołysania” Ziemi. Morze bliżej Księżyca - mocniej przyciągane, jest też bliżej wspólnego środka obrotu, więc mniej odpychane siłą odśrodkową. Po stronie przeciwnej, odwrotnie – grawitacja jest słabsza o tyle mniej więcej, o ile siła odśrodkowa jest większa. Równość tych ścierających się wpływów zawdzięczamy uśredniającemu działaniu masy całej Ziemi. Te dodatkowe siły w całej jej objętości muszą się znosić. To środek ciężkości Ziemi posłuszny drugiej zasadzie dynamiki wybiera tak zakrzywioną trajektorię w przestrzeni, by działające siły grawitacji były w równowadze z odśrodkowymi siłami bezwładności.
Z powyższych wywodów wynika, że na wodzie tworzą się dwie „górki” jedna po stronie Księżyca, druga po stronie przeciwnej.
Czy wszędzie na Ziemi występują dwa cykle pływowe na dobę?
Nie, nie wszędzie. Na biegunach nie ma w ogóle pływów dobowych, gdyż w wirowym ruchu dobowym Ziemi punkty biegunów w zasadzie nie poruszają się wzdłuż osi Ziemia-Księżyc (dr = const.). Leżą w tych samych położeniach na elipsoidzie powierzchni ekwipotencjalnej oceanu. Ponieważ jednak oś obrotu Ziemi nachylona jest do płaszczyzny orbity Księżyca, a Księżyc obiega Ziemię w ciągu 28 dni, więc w tym cyklu bieguny będą przemieszczały się na tle powierzchni tej elipsoidy - dr będzie się zmieniało. Wystąpią więc nieznaczne pływy miesięczne. Wskutek swego długiego okresu nie wywołają szybkich prądów pływowych i rezonansów piętrzących fale pływowe w pobliżu lądów, cieśnin, fiordów itp.
Wszędzie poza biegunami występować będą pływy dobowe na oceanach i otwartych morzach. Mniejsze lub większe ale będą.
Gdyby oś ziemska była prostopadła do płaszczyzny orbity Księżyca. Wtedy wszędzie (poza biegunami) i zawsze występowałyby dwa pływy na dobę. Jednak tak nie jest. Oś ziemska nachylona jest do płaszczyzny ekliptyki pod stałym kątem 23,5° a orbita Księżyca jest nachylona do ekliptyki pod kątem inklinacji 5,1°. Tej niewielkiej inklinacji zawdzięczmy stosunkowo częste zaćmienia. Ponieważ orbita Księżyca doznaje precesji o okresie 18,6 roku (6793 dni), więc kąt α nachylenia osi ziemskiej do orbity jest zmienny i waha się od 18,4° do 28,6° (23,5°± 5,1°). Nie wiem jaki jest dziś, ale i tak za kilka lat będzie inny. Księżyc okrąża Ziemię w ciągu 27,3 dni. W tym czasie kąt pomiędzy linią Ziemia-Księżyc a osią ziemską zmienia się w przedziale od 90°-α do 90°+α.
Kiedy kąt ten zbliży się do 90° (na rysunku oś ziemska pokryje się z linią pionową) wszystkie punkty na Ziemi będą w ruchu dobowym oscylowały wokół płaszczyzny przechodzącej przez środek Ziemi, prostopadłej do linii Ziemia-Księżyc. Dwa razy w ciągu doby będą w położeniach maksymalnych dla swego równoleżnika sił pływowych i dwa razy przejdą przez płaszczyznę zerowych sił pływowych.
Po 7 dniach (lub 7 dni wcześniej) kąt między linią Ziemia-Księżyc a osią ziemską osiągnie wartość 90°-α lub 90°+α (jak na rysunku). Wtedy wszystkie punkty na Ziemi, powyżej szerokości geograficznej 90°-α, będą w ruchu dobowym leżeć po jednej stronie płaszczyzny zerowych sił pływowych. Raz na dobę będą się zbliżać do niej osiągając minimum siły pływowej i raz na dobę oddalą się osiągając maksymalną dla swego równoleżnika wartość tej siły. Efekt pojedynczego pływu dobowego ujawnia się na szerokościach geograficznych 61,4° co 18,6 roku ale już powyżej 71,6° zawsze, co 14 dni. Będzie też zanikał ku biegunowi.
Zweryfikujmy tezę o pojedynczym cyklu pływów. Zrobiłem to przy pomocy programu MapSource i zestawu map Blue Chart Atlantic firmy Garmin. Poniżej widać tygodniową prognozę pływów od 17.07.2010 do 24.07.2010 dla Kap Morris Jesup na północy Grenlandii (N 83°,39’, W 33°50’).
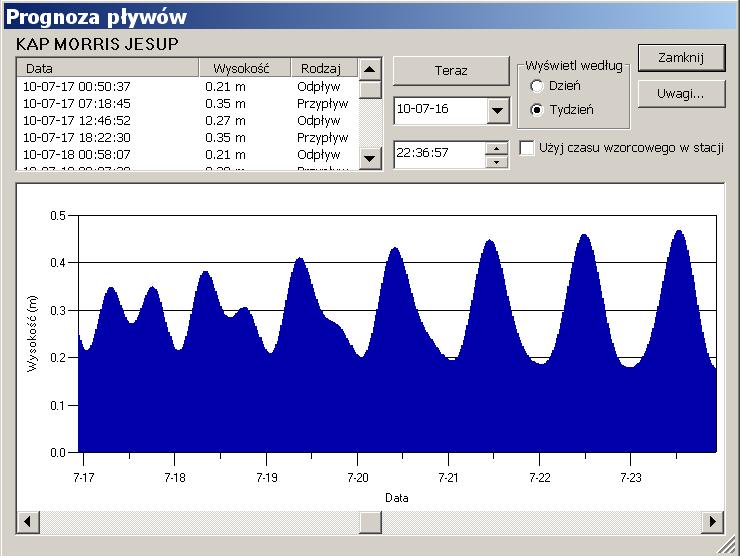
Dwa pływy na dobę na początku tygodnia przechodzą w jeden pływ, o większej amplitudzie, w jego końcu. Wzrost amplitudy też jest zgodny z teorią. Pływy są niskie co wynika z bliskości bieguna.
Czy amplitudy sąsiednich pływów są równe lub bliskie?
Jeśli oś ziemska jest ustawiona prostopadle do linii Ziemia-Księżyc, to oba dobowe pływy są podobne, gdyż wszystkie punkty Ziemi w swoim dobowym ruchu oddalają się od Księżyca o taką samą odległość dr poza środek Ziemi, o jaką zbliżają się po 12 godzinach do niego. Wtedy też występują najsilniejsze pływy na równiku i w szerokościach międzyzwrotnikowych, gdyż punkty równika przechodzą w ruchu dobowym przez punkty zenitu Z i nadiru N, a punkty bliskie równika w ich pobliżu.
Siedem dni wcześniej lub później, kiedy oś ziemska „patrzy” w kierunku Księżyca, tylko miejsca na równiku i w jego pobliżu oddalają się w ruchu dobowym o podobną odległość dr od środka Ziemi, od i ku Księżycowi, i tylko tam dwa pływy dobowe będą podobnej amplitudy.
Jacek Pasikowski