Anatomia fali - kinematyka

Przychodzą z wiatrem. Drobne zmarszczki rozbijają lustro wody. Początkowo nieodczuwalne dla łodzi, niezdolne nią poruszyć, jedynie igrają ze światłem, by po chwili pluskiem koić zmysły. Łagodne kołysanie wprawia w stan błogiego trwania, przechodzący z wolna w nudności. Kiedy cię wynicuje - wyda na poniewierkę członki, tłukąc w nie czym popadnie, zburzy pojęcie o przestrzeni i twoim w niej niezachwianym trwaniu, przerodzi niepewność w niepokój, który z hukiem walących się ścian wody ustąpi miejsca pewności, że właśnie wybiła ostatnia godzina. Ileż wrażeń, a jedna tylko, choć mnoga przyczyna. Kapryśna białogłowa, zdolna rozigrać blaskiem, rozmarzyć błękitem, rozkołysać i pogrążyć – fala.

Ci, którzy pływali po morzu wiedzą jak różnorodne bywa jego oblicze, jakie wywołuje uczucia: od błogości poprzez euforię, irytację, znużenie, po respekt i strach. To paradoksalne, ale wszystkie te uczucia zależą głównie od fal, ich wielkości, i kształtu, te z kolei zależą od siły wiatru, zmienności jego kierunku, wielkości i głębokości akwenu, bliskości brzegów, prędkości prądów. To z grubsza prawie każdy żeglarz wie, lecz czy zastanowiło Was kiedykolwiek, dlaczego fala ma taki kształt jaki ma? Dlaczego mała fala jest podobna sinusoidzie, a większa falbankom? Dlaczego się pieni na szczytach? Czy wiecie, że dłuższa wyprzedza krótszą? Dlaczego na płyciznach się załamuje? Nie jestem fachowcem w tych sprawach, ale mam trochę własnych przemyśleń, szczególnie po lekturze „Dzielności morskiej” Czesława Marchaja. Chcę się nimi podzielić.

Dla okazania istoty rzeczy wystarczy prosty przypadek fali płaskiej, nie wzbudzanej (martwej), na głębokiej wodzie.

Oscylacje harmoniczne

W szkole uczono nas, że drgania harmoniczne to periodyczne zaburzenie lub ruch mający tę właściwość, że wychyleniu (zaburzeniu) odpowiada wprost proporcjonalne do tego wychylenia przeciwdziałanie. Ruch ten dany jest zależnością:

$z(t)= A\sin(\omega t+\phi)$ (1)

gdzie z(t) jest wielkością zaburzenia o amplitudzie A, w chwili t, powtarzającego się z częstością ω. Kąt Φ nazywamy fazą początkową i jest wartością stałą. Jedyną zmienną niezależną jest czas. Równanie to opisuje ruch pojedynczego przedmiotu lub wartość zaburzenia w pojedynczym punkcie ośrodka. Dotyczy zatem drgań harmonicznych czegokolwiek, niekoniecznie rzeczy materialnych. Może to być dowolna zmienna fizyczna np. wektor pola, ciśnienie w przypadku fali akustycznej, potencjał elektryczny w przewodzie, składowa elektryczna lub magnetyczna fali elektromagnetycznej - radiowej, cieplnej, światła, promieniowania ultrafioletowego, rentgenowskiego, a jeśli dobrnęliście do podstaw fizyki kwantowej zapewne usłyszeliście o falach materii lub amplitudach prawdopodobieństwa. Wszystkie te zjawiska opisuje ta sama sinusoidalna zależność.

Można pominąć fazę początkową stwierdzając, że zaczęliśmy obserwację od fazy 0, kiedy zaburzenie z(0) = 0. To jest wyłącznie kwestia wyboru chwili rozpoczęcia liczenia czasu. Jeśli zaś ustalimy Φ = π/2 otrzymamy inną postać równania (1), również o zerowej fazie początkowej :

$z(t)= A\sin(\omega t+\frac{\pi}{2})= A\cos(\omega t)$ (1a)

Pewne obserwowane drgania są w przybliżeniu harmoniczne np. ruch wahadła w zakresie małych wychyleń. Tylko wtedy składowa siły grawitacji przeciwdziałająca wychyleniu jest do niego proporcjonalna. Rozwiązanie opisujące ruch wahadła podanym wyżej wzorem jest więc rozwiązaniem przybliżonym. Zwracam na to uwagę, by podkreślić, że przebieg realnych zjawisk fizycznych odbiega od wyidealizowanego ich opisu, posługującego się modelem, a znane rozwiązania obowiązują w ramach pewnych ograniczeń, o których często zapominamy.

Składanie oscylacji prostopadłych

Oscylacje można składać w różnych kierunkach, jednak szczególnie interesujące jest złożenie drgań prostopadłych z przesunięciem faz π/2. Jeśli złożymy wzajemnie prostopadłe drgania, to zaburzenie (ruch) będzie opisane dwoma równaniami - osobno dla współrzędnych y i z:

Ruch po okręgu:

$\left\{\begin{array}{ll}y=A\sin(\omega t+\frac{\pi}{2})\\z=A\sin(\omega t)\end{array}\right.\Leftrightarrow\left\{\begin{array}{ll}y=A\cos(\omega t)\\z=A\sin(\omega t)\end{array}\right.$ (2)

Ruch po elipsie:

$\left\{\begin{array}{ll}y=A_{y}\sin(\omega t+\frac{\pi}{2})\\z=A_{z}\sin(\omega t)\end{array}\right.\Leftrightarrow\left\{\begin{array}{ll}y=A_{y}\cos(\omega t)\\z=A_{z}\sin(\omega t)\end{array}\right.$ (2a)

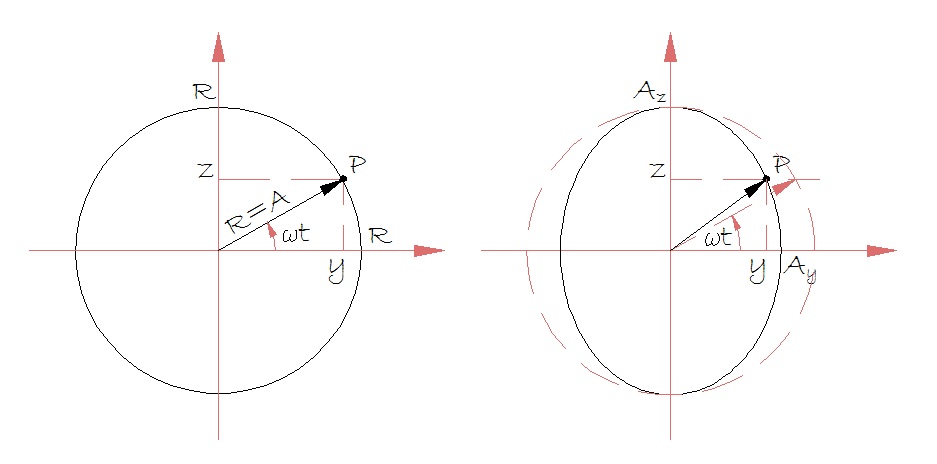
Rys. 1 Złożenie drgań harmonicznych wzajemnie prostopadłych, o przesunięciu fazowym π/2

Jeśli amplitudy A oscylacji w obu kierunkach są jednakowe, współrzędne y i z są współrzędnymi punktu poruszającego się po okręgu o promieniu R=A, z prędkością kątową ω (częstością), przeciwnie do ruchu wskazówek zegara. Faza ruchu ωt jest kątem wektora wodzącego. Jeśli ruch odbywa się w kierunku przeciwnym, to w równaniach ruchu fazę należy wziąć ze znakiem przeciwnym.

Złożenie drgań prostopadłych o różnicy faz π/2 i różnych amplitudach daje ruch po elipsie. W tym wypadku fazy ruchu ωt nie można utożsamiać z kątem wektora wodzącego.

Fale

Przyczyną drgań w pojedynczym obserwowanym punkcie ośrodka lub po prostu pustej przestrzeni, może być fala. Ruch falowy jest przemieszczającym się zaburzeniem o charakterze okresowym - często harmonicznym. Do opisu ruchu falowego nie wystarcza zatem jedna zmienna – czas. Potrzebne są również współrzędne położenia punktów drgających. Ilość współrzędnych zależy przede wszystkim od samego ośrodka. W przestrzeni trójwymiarowej potrzebujemy trzech współrzędnych, w membranach (elementach powierzchniowych - dwóch, a w środkach liniowych (strunach) – jednego.

W zależności od kształtu czoła fali ilość zmiennych położenia potrzebnych do opisu funkcji falowej można zredukować. I tak: ilość zmiennych przestrzennych fali o czole walcowym można zredukować do dwóch wymiarów (x, y) czyli tak jak dla fali powierzchniowej, a opis fali przestrzennej lub powierzchniowej o czole płaskim wymaga jednej zmiennej położenia (x) tak jak dla struny. Ponadto we współrzędnych biegunowych opis fal rozchodzących się kuliście i walcowo można zredukować do jednej zmiennej położenia (r).

Fale zasadniczo dzielimy na podłużne i poprzeczne. Słowo „zasadniczo” nie jest tu nieznaczącym wtrąceniem – przekonacie się przy omawianiu fal na wodzie. Fale podłużne to te, w których kierunek drgań jest zgodny z kierunkiem przemieszczania się fali. Przykładem jest fala akustyczna. Ruch drgający cząstek powietrza odbywa się w kierunku ruchu fali. Fale w drgających poprzecznie membranach i strunach, czy elektromagnetyczne są falami poprzecznymi. W przypadku fal elektromagnetycznych właściwie jest to złożenie ściśle od siebie zależnych drgań pola elektrycznego i magnetycznego. Oscylacje składowej elektrycznej i magnetycznej odbywają się w kierunkach wzajemnie prostopadłych i są przesunięte w fazie o π/2 czyli kąt prosty jak na rys. 1. Poprzeczne fale mechaniczne w strunach również można wywołać jednocześnie w dwóch dowolnych kierunkach płaszczyzny prostopadłej do struny, nie tylko pod kątem prostym. Nazywamy to składaniem fal, a zależności nimi rządzące są analogiczne jak przy składaniu drgań pojedynczego punktu, tylko równania opisujące je będą równaniami falowymi, zależnymi nie tylko od czasu lecz również współrzędnych przestrzennych położenia.

Fale płaskie poprzeczne

W dalszych rozważaniach będziemy się zajmowali falą płaską, czyli taką, której czoło jest płaskie, prostopadłe do kierunku poruszania się fali. Opis fal mechanicznych poprzecznych o wychyleniu w kierunku osi z w trójwymiarowym układzie współrzędnych można wtedy zredukować do dwóch wymiarów, gdyż w trzecim wymiarze, prostopadłym do kierunku ruchu fali i prostopadłym do kierunku drgań opis ruchu jest identyczny. Przyjmiemy płaski układ współrzędnych, skierowany osią x (zmienna położenia) w kierunku ruchu fali, a osią z w kierunku prostopadłym do x.

Jeśli chcielibyśmy znać wielkość „wychylenia” fali poprzecznej w dowolnym miejscu i dowolnej chwili, to musimy wyrazić z nie tylko w postaci funkcji czasu t, ale również położenia x. Trzeba jednak znać przynajmniej długość fali L, jej okres T, lub prędkość rozchodzenia się c. Zaburzenie w danym punkcie przyjmuje tę samą wartość co czas równy okresowi T, a w ustalonej chwili czasu - w punktach leżących od siebie w odległości L. To właśnie wyraża poniższe równanie. Podstawienie do niego w miejsce t wartości t+nT lub w miejsce x wartości x+nL, gdzie n jest dowolną liczbą całkowitą, daje to samo równanie.

$z(x,t)= A\sin(2\pi\frac{t}{T}- 2\pi\frac{x}{L})$ (3)

Uwzględniając, że $\frac{2\pi}{T}= \omega$ i wprowadzając wielkość $\frac{2\pi}{L}= k$ (tzw. długość wektora falowego) uzyskamy:

$z(x,t)= A\sin(\omega t-kx)$ (4)

Skoro $c=\frac{L}{T}$ to można zapisać $k=\frac{2\pi}{L}=\frac{2\pi T}{TL}=\frac{\omega}{t}$ , a zatem:

$z(x,t)= A\sin\Big(\omega(t-\frac{x}{c})\Big)$ (5)

To kilka postaci tego samego równania falowego. Zapamiętajmy, że kąt (argument funkcji sinus), utożsamiamy z fazą ruchu oscylacyjnego.

Fale na wodzie

Jaką falą jest fala na wodzie? Dziwną. Większość ludzi sądzi chyba, że poprzeczną. To półprawda – właściwie trzecia z prawd księdza Tischnera. Powierzchnia wody oscyluje w kierunku pionowym, a fala rozchodzi się poziomo - jak w fali poprzecznej, ale prawa dynamiki nie opisują ruchu powierzchni, a ruch mas, czyli cząstek wody i to one oscylują. Z literatury wiadomo, że cząstki wody wykonują ruch rotacyjny po okręgu, ze stałą prędkością kątową. Czy to precyzyjne stwierdzenie - okaże się później. Składowa pionowa tego ruchu jest prostopadła do kierunku ruchu fali, ale druga składowa – pozioma, jest do niego równoległa. Nie jest to więc klasyczna fala poprzeczna, a złożenie fali podłużnej i poprzecznej, o przesunięciu fazowym π/2, skoro to ruch po okręgu.

Jeśli chodzi o dynamikę ruchu, to fale na wodzie są falami powierzchniowymi, których propagacja zależy od siły grawitacji. To ona wyznacza kierunek drgań poprzecznych ośrodka i w kierunku jej działania przyjmiemy oś z, o zwrocie do góry. Siła grawitacji również wyznacza poziomą płaszczyznę lustra wody, więc powierzchnię xy ruchu fal. Gdyby nie grawitacja nie byłoby rozprzestrzeniania się fal po powierzchni wody, chyba że tych które propagują przez napięcie powierzchniowe – te jednak nas nie interesują. Z tej przyczyny fale na wodzie nazywa się falami powierzchniowymi grawitacyjnymi. Nie mylmy ich jednak z jeszcze nie wykrytymi, choć przewidywanymi ogólną teorią względności zaburzeniami pola grawitacyjnego.

Ponieważ interesują nas głównie fale z jakimi „walczą” łodzie i statki, ograniczymy się do nieco wyidealizowanej sytuacji ruchu fal płaskich. Ich cechą jest to, że poruszają się w jednym kierunku - przyjmiemy, ze wzdłuż osi x. Realnie kierunek ten wymusza głównie kierunek wiatru. Nie rozchodząc się koncentrycznie tak jak fale koliste, fale płaskie powoli rozpraszają swoją energię. Na razie pominiemy tłumienie. Jeśli chodzi o zrozumienie istoty rzeczy, takie przybliżenia są satysfakcjonujące.

Na powierzchni

Jak wygląda kształt takiej fali? Załóżmy wstępnie, że cząstki wody krążą po okręgu ze stałą prędkością kątową i zobaczmy co z tego wyniknie. Wyznaczymy położenia cząstek wody na jej powierzchni, w ich ruchu rotacyjnym w jednej chwili. Niejako zamrażamy lub fotografujemy profil fali. Skonstruujmy krzywą kształtu fali, dzieląc jej długość np. na 12 równych odcinków i na tyle samo części dzieląc okrąg o promieniu R, aby wyznaczyć 12 kolejnych faz pełnego cyklu. Zaczniemy naszą konstrukcję od prawego szczytu fali. W tym miejscu „element” wody na powierzchni zajmuje najwyższe położenie w swym ruchu rotacyjnym i do tej początkowej fazy ruchu odniesiemy wszystkie 12 faz punktów rozmieszczonych równomiernie na długości fali w lewo od prawego szczytu.

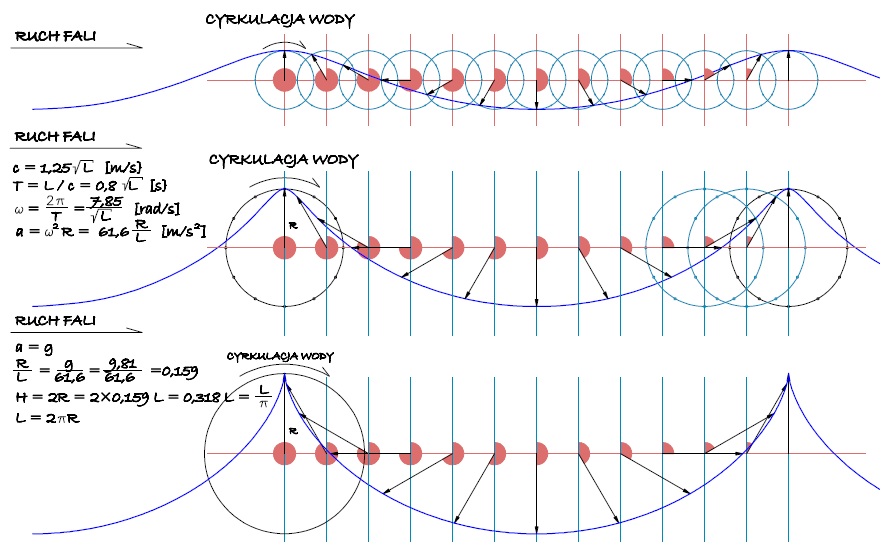
Rys. 2 Konstrukcja powierzchni fali: szkic 1 – fala łagodna, szkic 2 – fala stroma, szkic 3 – sytuacja graniczna

Pierwszy punkt na lewo od prawego szczytu fali leży w odległości 1/12 jej długości. Szczyt fali minął go 1/12 okresu temu, czyli od tamtego momentu do chwili obecnej cząstka wody pokonała 1/12 pełnej cyrkulacji i teraz jest w fazie 2π/12 = π/6 = 30°. To samo otrzymamy z równania falowego (3) podstawiając t=0 i x=-L/12: 2πt/T - 2πx/L = 2π0/T - 2π(-L)/12L= π/6. O tyle obracamy wektor wodzący. Jego koniec wyznacza obecne położenie cząstki wody. Drugi punkt na lewo od prawego szczytu fali leży w odległości 2/12 długości fali i szczyt fali minął go 2/12 okresu cyrkulacji wcześniej, więc element powierzchni wody jest teraz w fazie późniejszej o 2/12 = 1/6 pełnego obiegu, czyli 2π/6 = π/3 = 60°. Cofając się dalej w lewo rysujemy wektory wodzące kolejnych okręgów w fazach coraz późniejszych, aż dojdziemy do lewego szczytu fali. Tak wyznaczone wektory wskazują położenia elementów powierzchni wody w jednej chwili. Po połączeniu ich końców gładką krzywą otrzymujemy kształt fali. Kolejną konstrukcję przeprowadziłem dla cyrkulacji o dwa razy większym promieniu. O ile na pierwszym szkicu fala jest zbliżona kształtem do sinusoidy, w drugim przypadku asymetria kształtów grzbietów i dolin jest wyraźna, tak jak to obserwujemy w rzeczywistości. Oto więc odpowiedź na pytanie dlaczego szczyty większych fal są krótkie i strome a doliny szerokie i łagodne. Wszystkiemu winna składowa pozioma ruchu cząstek wody w ich cyrkulacji, a więc ta, która jest składową podłużną drgań. Gdyby cząstki wody poruszały się jedynie w pionie fale byłyby sinusoidami.

Sądzicie, że taką konstrukcję można przeprowadzić dla dowolnie dużego promienia cyrkulacji, czyli dowolnie wysokiej fali? Jeśli zwiększymy długość fali, proporcjonalne powiększenie jej wysokości sprowadza się do przekształcenia całej konstrukcji przez jednokładność. Konstrukcja pozostanie niezmieniona. Natomiast przy ustalonej długości fali, powiększanie promienia prowadzi do uzyskania kształtów fal, jakich nie obserwujemy w naturze, tak jak na trzecim szkicu. W tej konstrukcji specyficzne jest to, że stosunek L/R = 2π czyli obwód okręgu rotacji jest równy długości fali. Oznacza to, że prędkość liniowa cyrkulujących cząsteczek wody jest równa prędkości fali. Ponadto zauważcie, że w samym szczycie fali trajektorie cząstek wznoszących się i opadających pokrywają się. To kolizja – istotne ograniczenie – rzecz niemożliwa w naturze. Próbując konstruować coraz wyższe w stosunku do długości fale w pewnym momencie zaczynamy fantazjować – konstrukcja traci związek z rzeczywistością. W którym?

Kiedy już znamy sposób konstruowania kształtu fali zauważymy, że uzyskana krzywa jest zakreślana przez obracający się wektor o długości R, którego początek przemieszcza się ze stałą prędkością c po osi x, gdzie c jest prędkością przemieszczania się fali. Łatwo zdefiniować tę krzywą w postaci parametrycznej.

$\left\{\begin{array}{ll}x=ct+x\cos(\omega t)\\z=R\sin(\omega t)\end{array}\right.\Leftrightarrow\left\{\begin{array}{ll}x=\frac{L}{T}t+R\cos(\omega t)\\z=R\sin(\omega t)\end{array}\right.\Leftrightarrow\left\{\begin{array}{ll}x=\frac{\omega t}{k}+R\cos(\omega t)\\z=R\sin(\omega t)\end{array}\right.$ (6)

Te równania opisują cykloidę czyli krzywą zakreślaną przez punkt na toczącym się kole. Czy istnieje postać jawna z = f(x)? Ja jej nie znam. W literaturze spotkacie nieco inne równania i krzywe w lustrzanym odbiciu względem bieżni, co wynika z faktu, że tam koło toczy się „po bożemu” po ziemi, a nie po suficie, a układ współrzędnych związany jest właśnie z bieżnią, a nie z trajektorią środka koła jak u nas.

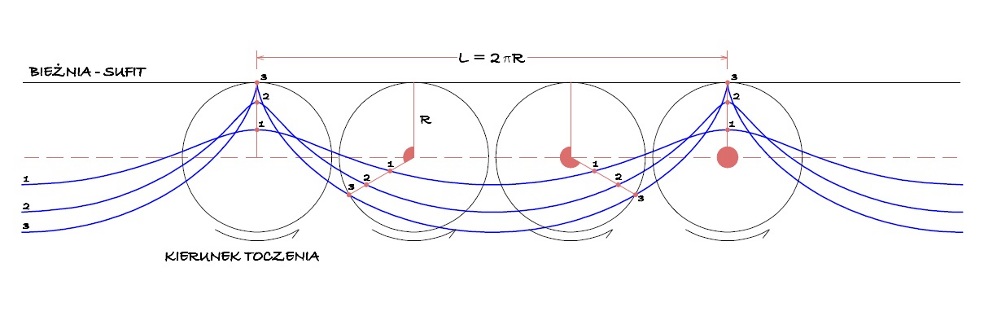
Rys. 3 Cykloidy, zakreślane przez punkty na kole toczącym się po „suficie”, dokładnie oddają kształty skonstruowane na rys. 2

Czas już na ważną dygresję. Wszystko do czego do tej pory doszliśmy wynika z przyjętej a’priori kinematyki ruchu wody. Założyliśmy, że ruch odbywa się po okręgu i założenie to nie wynika z żadnych równań dynamiki, równań ciągłości ośrodka, warunków jego nieściśliwości. Zatem założenie o ruchu po okręgu, w jakimś przybliżeniu zapewne prawdziwe, nie musi być ścisłe.

Wspomniane wcześniej ograniczenie wynika również z rozważań dynamicznych. Teoria mówi, że prędkość rozchodzenia się fal na wodzie dana jest tzw. związkiem dyspersyjnym:

$c=\sqrt{\frac{g}{k}}= \sqrt{\frac{gL}{2\pi}}= \sqrt{\frac{9.81}{2\times 3.14}}\sqrt{L}= 1.25\sqrt{L}$ (7)

(zaniedbano lepkość i napięcie powierzchniowe, wielkości fizyczne w jednostkach układu SI [kg,m,s])

Na rysunku 2, wyprowadziłem z tej zależności wzór na przyspieszenie dośrodkowe (odśrodkowe), ale tutaj zrobię to na liczbach ogólnych wykorzystując zależność (7) c² = g/k:

$a=\omega^2 R=(\frac{2\pi}{T})^2 R=(\frac{2\pi L}{LT})^2 R=\frac{(2\pi)^2}{L^2}c^2 R=\frac{(2\pi)^2}{L^2}\frac{g}{k}R=\frac{(2\pi)^2}{L^2}\frac{gL}{2\pi}R=2\pi g\frac{R}{L}$ (8)

Jeśli podstawimy L=2πR (obwód okręgu równy długości fali) otrzymamy:

$a=g\frac{2\pi R}{L}= g\frac{2\pi R}{2\pi R}= g$ (9)

Szkic 3 na rysunku 2 lub cykloida 3 na rysunku 3 przedstawiają tę sytuację. Przyjrzyjmy się temu baczniej. Z zależności (9) widać, że w przyspieszenie dośrodkowe jest równe ziemskiemu, a w szczycie fali skierowane jest w dół, co oznacza, że cząstki wody są tam w stanie swobodnego spadku. Woda niejako traci swój ciężar, nie wywiera ciśnienia na inne cząstki, tracąc również właściwość wypierania ciał o mniejszym ciężarze właściwym, a więc również powietrza. Trafiliśmy chyba na ślad grzywacza! Ponadto znaleźliśmy istotne ograniczenie z góry: wysokość fali nie może być większa od L/π bo w szczycie cząstki nie mogą poruszać się z przyspieszeniem dośrodkowym większym od ziemskiego – wszak działa na nie tylko ciążenie. To ograniczenie wysokości nie dotyczy prawdopodobnie fal przybojowych – załamujących się. Pamiętajmy jednak, że nasze rozumowanie oparte na założonej kinematyce ruchu nie jest ścisłe i może istnieć bardziej radykalne ograniczenie wysokości fali. W zasadzie z kształtu piku na szczycie fali można wnosić, że musi być znacznie ostrzejsze ograniczenie wynikające z prawa ciągłości strugi (ośrodka). W szczytowym piku trajektorie wody wznoszącej się i opadającej zbiegają się do punktu - są do siebie styczne, co oznacza kolizję. To musi prowadzić do turbulencji przy znacznie niższej fali, gdy sytuacja taka jeszcze nie zachodzi. Fala w turbulencjach grzywacza traci nadmiar energii i obniża się. Gdy opadnie na tyle, by ruch wody w szczycie stał się znów laminarny, kumuluje energię oddziaływania wiatru i znowu w kolejnym grzywaczu traci ją.

Z zależności (8) wynika, że przyspieszenie odśrodkowe cyrkulacji wody jest proporcjonalne do R/L, co oznacza, że pływające na powierzchni wody przedmioty będą doznawały takich samych przyspieszeń na falach dużych i małych, o ile stosunek wysokości do długości fal H/L (stromość) lub R/L będzie identyczny, a więc ich kształty, będą podobne. Dalej będę używał sformułowania „strome” a nie „wysokie” fale, bo nie wysokość fali jest istotna, a proporcja wysokości do długości.

Próba dalszego ekstrapolowania pokazanej na rysunku 2 konstrukcji geometrycznej poprzez powiększanie promienia rotacji prowadzi do powstania „pętelki” na szczycie fali, czyli przecięcia się torów cząstek wody wstępujących z opadającymi, co w naturze, ani nawet w teorii, nie jest już możliwe.

W tych konstrukcjach dla stromych fal jest jednak coś niepokojącego. Jeśliby utożsamić linię łączącą środki okręgów z powierzchnią spokojnej, niesfalowanej wody to mielibyśmy do czynienia z ubytkiem wody w akwenie. O wiele mniej wody wypełnia szczyt stromej fali, ponad tą linią niż ubyło w dolinie. Różnica jest tym większa im bardziej stroma jest fala. Musimy dojść zatem do wniosku, że linia środków cyrkulacji nie jest linią powierzchni spokojnej wody – poziomu morza, że w miarę podwyższania się fal, środki cyrkulacji podnoszą się, na tyle aby zachować warunek stałej objętości wody, czyli to co wystaje ponad poziom morza musi być co do objętości równe temu czego brakuje poniżej tego poziomu i tym sposobem szczyty fal są wyższe niż doliny głębokie, choć ich objętości są równe. Należałoby zatem poprawić nieco naszą konstrukcję czyniąc zadość zasadom ciągłości i nieściśliwości ośrodka. Aby to uczynić należy spojrzeć w głąb fal, by zaobserwować co dzieje się z objętością falujących wód.

W głębi

Zdajemy sobie sprawę z tego, że falowanie zanika wraz z głębokością. Kto nurkował - ten wie. W książce Marchaja można przeczytać, że przy wzroście głębokości o 1/9 długości fali, promień cyrkulacji maleje o połowę. Funkcja wykładnicza ma tę własność, że dla rzędnych różniących się o tę samą wartość stosunek wartości funkcji jest stały. Falowanie zanika więc wykładniczo. Ponieważ ta 1/9 wydaje się być jedynie przybliżeniem, znalazłem wyprowadzenie równań ruchu cząstek wody w „Hydrodynamice” Landaua i Lifszyca dla akwenu o dużej głębokości. Z równań tych wynika, że R(z) maleje wykładniczo, asymptotycznie do zera kiedy wysokość z dąży do -∞ (oś z skierowana w górę), a funkcja ta, wygląda następująco:

$R(z)= R(0)e^{kz}$ (10)

Zatem dla jakiej różnicy głębokości z-z₁ (z > z₁) stosunek amplitud jest dwukrotny?

$\frac{R(z)}{R(z_1)}= \frac{R(0)e^{kz}}{R(0)e^{kz_1}}= e^{k(z-z_1)}= 2\hspace{0.5cm}\Leftrightarrow\hspace{0.5cm}k(z-z_1)=\ln 2\hspace{0.5cm}\Leftrightarrow\hspace{0.5cm}z-z_1=\frac{\ln 2}{k}= \frac{\ln 2}{2\pi}L=\frac{0.6931}{6.283}L=\frac{1}{9.065}L$ (11)

Faktycznie jest to liczba bliska 1/9 długości fali.

Wyobraźmy sobie, że rozpinamy w wodzie pionową, rozciągliwą sieć lub lepiej - barwimy poziome i pionowe ścieżki wody, po czym obserwujemy jak zachowuje się taka sieć w rozfalowanej wodzie. Stosując dotychczasową konstrukcję i zaczerpniętą zasadę wykładniczego zaniku falowania wraz z głębokością uzyskamy obraz taki jak poniżej.

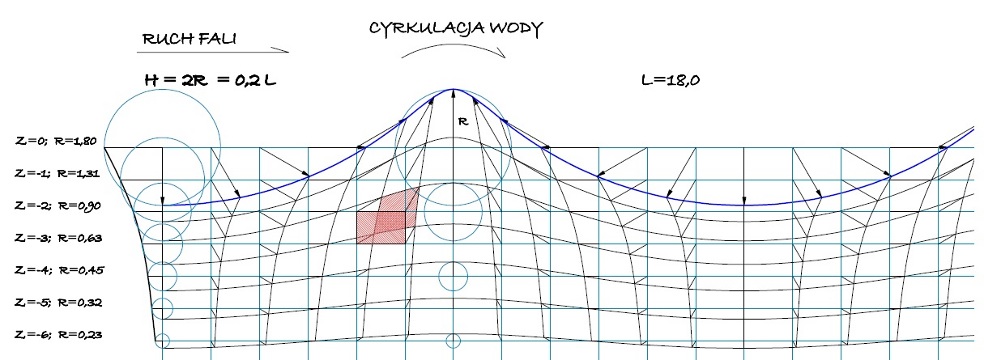
Rys. 4 Obraz deformacji siatki elementów skończonych, ilustrujący przemieszczenia cząstek wody w fali – konstrukcja geometryczna.

Jak już wspomniałem taka konstrukcja ujawnia „defekt masy” wody. Szczyty ponad liną środków okręgów zawierają mniej wody niż ubyło jej z dolin poniżej niej. W głębszych warstwach efekt ujawnia się również, ale już na głębokości 1/3 długości fali (na rys 4. z = -6m) jest prawie niedostrzegalny. Im bardziej warstwa jest pofalowana, tym bardziej niedobór się uwidacznia. Ponieważ warstwy leżą na sobie, niedobory objętości sumują się. Konstrukcja oparta na kołowych cyrkulacjach wokół początkowych punktów równowagi kłóci się z zasadą zachowania masy. Jeśli ciecz jest nieściśliwa, każdy z elementów sieci ma stałą gęstość czyli również masę. Suma objętości elementów w obrębie warstwy również musi być stała, a widzimy, że nie jest. Czyżby konstrukcja była niepoprawna? Na pewno jest niedokładna.

Mit

Niewiele mówi się o falach podczas szkoleń żeglarskich. Prawda o kołowych cyrkulacjach z mocą dogmatu podawana jest adeptom. Oczywiście nie jestem znawcą tematu i nie studiowałem wcześniej literatury, zajmującej się ruchem falowym wody, zadziwia mnie jednak, że przez lata nie spotkałem wzmianki, że coś w kwestii cyrkulacji wody jest nie tak, że jakaś nieścisłość wkrada się do opisu. Nawet tak poważne prace jak wspomniana „Hydrodynamika” Landaua i Lifszyca podają rozwiązanie równań ruchu fali płaskiej grawitacyjnej dla małych, w stosunku do długości, amplitud fal. Rozwiązanie podał już prawdopodobnie Euler, tak dawno temu, że trudno byłoby uwierzyć, że problem stromych fal nie został od tamtej pory zbadany. Dlaczego więc wiedza o tym nie weszła do kanonu? Może jest niepotrzebna dla zrozumienia podstawowych kwestii? Może osobiste doświadczenie jest tu wystarczające i dużo bardziej znaczące dla człowieka morza? Ja to wszystko rozumiem, ale to jednak dla mnie trochę irytujące, że korzystamy z opisu nieadekwatnego do interesujących nas sytuacji, nawet nie przeprowadzając krótkiej dyskusji błędów. Jeśli żeglarz, szyper, projektant zajmuje się falami i próbuje dociec co zagraża jego łodzi, zrozumieć jej zachowanie, to nie interesują go małe fale. Wszystkie właściwie dociekania dotyczące zachowania się statków, łodzi, jachtów na falach dotyczą fal dużych i stromych. Fale łagodne interesują nas o tyle, o ile są nużące i wywołują nudności.

Szukałem w Internecie, niezbyt długo, dokładniejszego opisu dużych fal – nie znalazłem nic. Wszystkie znalezione rozwiązania dotyczące fal grawitacyjnych na wodzie głębokiej, w kanałach, płytkich wodach, bazują na założeniu małych amplitud. Po prostu takie założenie pozwala pominąć, jako nieskończenie mały wyższego rzędu, pewien składnik równania ciągłości ośrodka (zachowania masy), co upraszcza równanie różniczkowe i daje stosunkowo proste rozwiązanie harmoniczne. Wyprowadza się stąd również związek dyspersyjny, a z niego zależność prędkości fal od ich długości, który jest przywoływany w literaturze bardzo powszechnie. Jednocześnie nie spotkałem w popularnej literaturze żeglarskiej, choćby śladu wzmianki na temat zakresu stosowania tej zależności.

Postanowiłem poszukać sam lepszego opisu dla stromych fal. Nie podejmuję się rozwiązać dokładnego równania różniczkowego. Spodziewam się, że rozwiązanie nie jest proste, skoro trudno je napotkać nawet w literaturze fachowej. Dla dużych wychyleń wahadła matematycznego (zadania znacznie prostszego, w którym jednak dostrzegam pewną analogię do fal) rozwiązanie jest nieskończonym szeregiem. Nie spodziewam się zatem w przypadku fal rozwiązania w postaci jakiejś prostej jawnej funkcji. Jeśli zaś rozwiązanie jest szeregiem to zastosowanie go zmusza do liczenia kolejnych przybliżeń. Znalezienie zatem lepszego przybliżenia wydało mi się kuszące. Nie interesuje mnie bardzo precyzyjny opis, a jedynie taki, który w całym obszarze od nieskończenie małych fal, do fal szczytujących z przyspieszeniem ziemskim nie generuje bzdur. Nie wiedziałem czy dojdę do czegoś, ale wiedziałem, że na pewno będę miał frajdę. Postanowiłem jednak spróbować inaczej niż Wielcy – nie z wyżyn matematycznej analizy rozbierać równania, a prostacko, po inżyniersku przyjrzeć się i „zgadnąć” rozwiązanie. Oczywiście parę wzorków trzeba oswoić i zakląć, lecz to już „sam miód”.

Globalny defekt masy

W pokazanych na rys. 2 i 4 konstrukcjach fal cząstki krążą wokół początkowych położeń równowagi o współrzędnych x,z. Położenia jakie zajmują w ruchu kołowym X, Z w dowolnej chwili czasu można wyznaczyć ze wzorów (2a) oraz (4). Ponieważ rotacja cząstek wody odbywa się w kierunku przeciwnym niż w lewoskrętnych układach współrzędnych, do jakich jesteśmy przyzwyczajeni z lekcji matematyki, więc fazę ruchu zapisujemy ze znakiem przeciwnym.

$\left\{\begin{array}{ll}X-x=R_x(z)\cos(k x-\omega t)\\Z-z=R_z(z)\sin(k x-\omega t)\end{array}\right.$ (12) uwzględniając wykładniczy zanik oscylacji zgodnie z (10)

$\left\{\begin{array}{ll}X=x+R e^{kz}\cos(k x-\omega t)\\Z=z+R e^{kz}\sin(k x-\omega t)\end{array}\right.$ (13)

Spójrzmy na powierzchnię fali. To, co wystaje ponad lustro spokojnej wody, powinno być równe co do objętości temu, czego ubyło poniżej lustra. Tak niestety nie jest. To samo można powiedzieć o głębszych warstwach. Ujawnia się „defekt” masy. Proszę się nie obawiać, nie chodzi o syntezę jądrową. Defekt ten zanika z głębokością, bo amplituda fal się zmniejsza, a kształty łagodnych fal są bliższe sinusoidom. Wartość średnia funkcji sinus w przedziale równym jej okresowi jest równa 0. Tak być musi, bo sinus jest funkcją nieparzystą czyli symetryczną względem początku układu współrzędnych. Po prostu dolina i górka mają ten sam, lecz odwrócony kształt. Niedobór wody ujawnia się w warstwach powierzchniowych. Im bardziej są pofałdowane tym jest on większy. Jak to skorygować najmniejszym kosztem, nie burząc całkiem teorii? Faliste powierzchnie graniczne warstw trzeba podnieść tak, by każda warstwa miała objętość równą swojej objętości początkowej w stanie niepofalowanym. Jest to równoważne podniesieniu środków cyrkulacji cząstek, tym większe im są płycej, czyli im bardziej są odkształcone falami. Znaczy to, że oscylacje cząstek nie będą się odbywały wokół początkowych położeń równowagi, ale kto powiedział, że tak być musi? Ktoś powie - Euler. Tak, ale on podał rozwiązanie tylko dla fal o małej w stosunku do długości amplitudzie, a nasze takie nie są.

Postanowiłem wyliczyć jakie podniesienie powierzchni granicznych, a więc środków rotacji węzłów siatki, zachowa pola warstw. Do tego posłużył mi arkusz kalkulacyjny, bo liczenie powierzchni dużej ilości czworokątów nieforemnych i sumowanie ich znacznie przekracza granice mojej determinacji. Procedura obliczeniowa daje w wyniku korektę współrzędnych środków cyrkulacji, wyliczanych z kryterium zachowania objętości każdej z warstw. Czyni to iteracyjnie, dzięki odwołaniom cyklicznym (komórki odwołują się pośrednio do samych siebie). W każdym kroku wyliczane są poprawki, o które korygowane są dane wyjściowe - współrzędne zetowe środków rotacji węzłów. Oto ilustracja wyników:

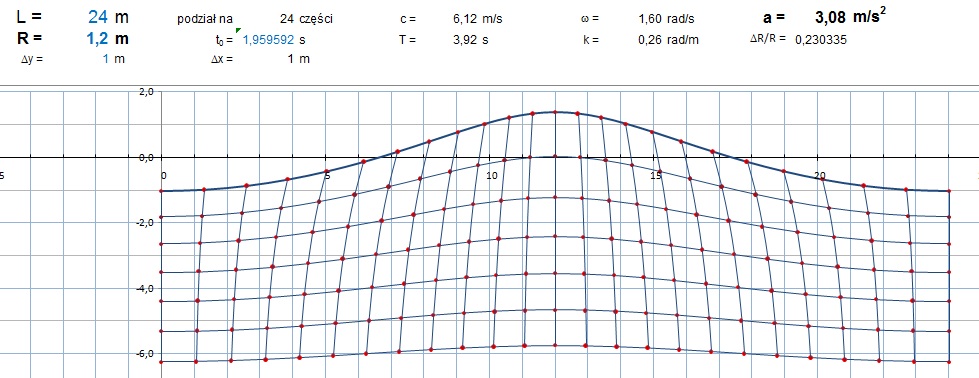
Rys. 5 Konstrukcja fali H/L = 0,1 (R/L=0,05) z korektą objętości warstw - podniesienie środka cyrkulacji powierzchni o 0,078 H (0,155 R)

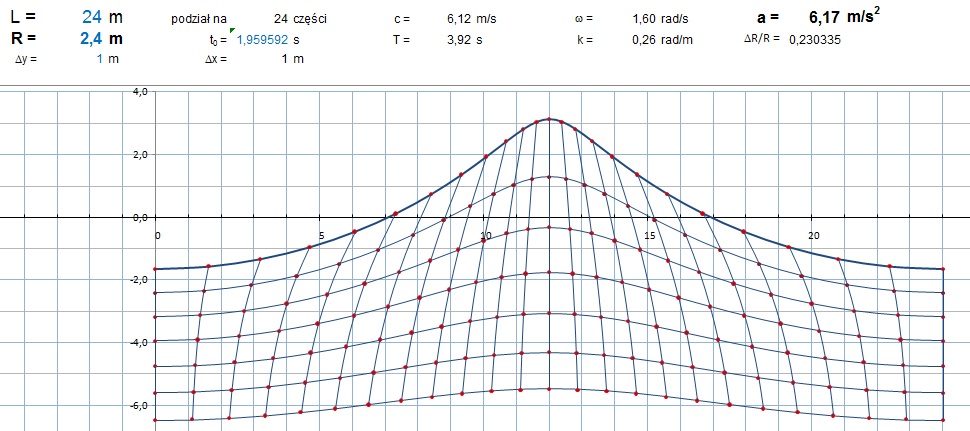
Rys. 6 Konstrukcja fali H/L = 0,2 (R/L=0,1) z korektą objętości warstw - podniesienie środka cyrkulacji powierzchni o 0,155 H (0,310 R)

Teraz widać, że szczyty fal wystają wyżej ponad początkowe lustro wody niż doliny się pod nie zagłębiają. Obliczenia przeprowadzone dla różnych długości i wysokości fal wykazują, że względne podniesienie środka cyrkulacji ΔZ/R, cząstek wody dowolnej powierzchni potencjalnej jest proporcjonalne do R/L, przy czym R jest promieniem cyrkulacji dla tej powierzchni.

$\frac{\Delta Z}{R}= 3.106\frac{R}{L}$ lub $\Delta Z=3.106\frac{R^2}{L}$ (14)

Pojawiła się dziwna liczba - stały dla wszystkich symulowanych przypadków współczynnik proporcjonalności. Bez względu na wartości zmiennych R i L arkusz kalkulacyjny z uporem maniaka wylicza wciąż 3,105828541… Ktoś ma pomysł co to za liczba? Jest dziwnie bliska π Ważny trop czy przypadek? Ubytek wody na długości fali ΔZ L byłby równy polu cyrkulacji πR²? Zauważmy, że zależność (14) obowiązuje dla każdej granicy warstw wody, nie tylko dla jej powierzchni. Wystarczyłoby przecież „zdjąć” górną warstwę i kolejna stałaby się powierzchnią. Konstrukcja jest identyczna dla warstwy powierzchniowej jak i każdej innej. Zmienia się jedynie promień rotacji. Sumowanie powierzchni czworokątów jest przybliżonym obliczeniem powierzchni warstwy, a zastosowany podział na 24 części nie jest szczytem dokładności. Dziwne, że „odkryta” stała jest wyliczana z tak wielką dokładnością (sprawdzałem do 10 cyfr znaczących). Przybliżenie krzywej łamaną może dawać istotną rozbieżność od wartości π Przypominam, że wszystkie założenia o kinematyce ruchu do tej pory były przyjęte z góry, jedynie funkcję zanikania fal z głębokością zweryfikowaliśmy z rozwiązaniami ruchu falowego dla małych amplitud. Zorientowałem się przy okazji, że mam oto świetne narzędzie nie tylko do symulacji, ale także, przez zastosowanie wykresów, do wizualizacji.

Lokalny defekt masy

Wygląda na to, że dzięki podniesieniu środków cyrkulacji udało się uratować założenie, że cząstki wody krążą po okręgach ze stałą prędkością. Niestety, jeśli przyjrzeć się bliżej powierzchniom pól poszczególnych oczek siatki – okaże się, że nie. Suma w obrębie warstw zgadza się bardzo precyzyjnie, ale poszczególne pola różnią się od początkowych: w przypadku fali z rys 6 (H/L=0,2) - do 20,8%; w przypadku fali z rys 5 (H/L=0,1) - do 8,7%. Niestety różnica jest niebagatelna i oznacza, że w przypadku stromych fal założenie o ruchu po okręgu ze stałą prędkością kątową załamuje się. Było to widać zresztą po kształcie cykloidy trzeciej. W dolinach mamy do czynienia z nadmiarami powierzchni oczek sieci, a w szczytach z niedoborami pól. W szczytach elementy powinny być nieco szersze, a w dolinach węższe, aby zachować stałe powierzchnie. Mogłoby to oznaczać, że amplituda składowej poziomej cyrkulacji powinna być mniejsza od amplitud pionowych. Ruch o ile miałby być harmoniczny, musiałby odbywać się po elipsie o pionowej osi długiej. Można też próbować zmieniać w czasie prędkość czyli częstość w ruchu rotacyjnym, ale na razie wara od świętości harmonicznej. Przyjmując zasadę najmniejszych strat trzeba zapytać: Co możemy uratować z pierwotnych założeń? Z których najmniejszym kosztem można się wycofać? Wydaje się, że przyroda „lubi” oscylacje harmoniczne, ich łagodne, faliste, cyklicznie różniczkowalne rozwiązania. Ruch po elipsie wydawał się łatwo akceptowalną, mało inwazyjną modyfikacją. Trzeba przy tym pamiętać, że „lepsze” przybliżenie powinno zbliżać się do pierwotnego dla łagodnych fal, bo dla nich pierwotne rozwiązanie jest ścisłe – wyprowadzone z równań dynamiki, zachowania masy, ciągłości ośrodka i warunków brzegowych. Wraz z głębokością mimośrody elips powinny się zatem zmniejszać, by trajektorie ruchu zbliżały się kształtem do okręgów. Można się spodziewać, że dzieje się to wykładniczo, tak jak zanika amplituda falowania. Takie, założenia pociągają za sobą względnie małe „koszty”. Po kilku próbach, korektach znalazłem dość eleganckie rozwiązanie poprawiające dokładność opisu.

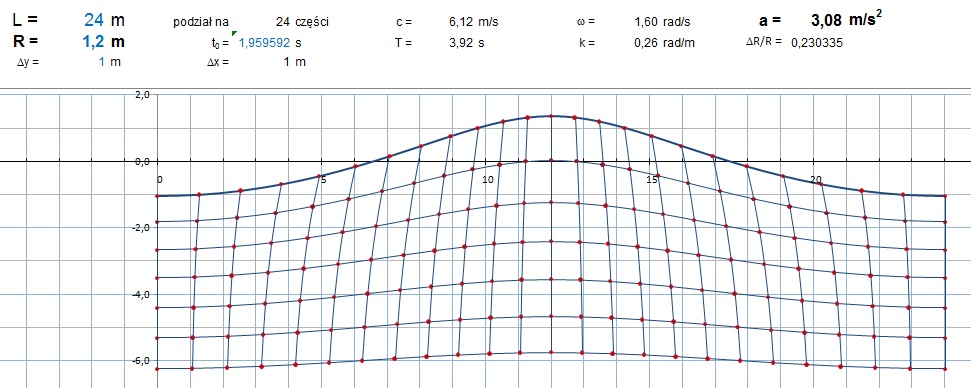
Rys. 7 Konstrukcja fali H/L = 0,1(A_z/L=0,05) z cyrkulacją eliptyczną i podniesieniem środków cyrkulacji o πA_zA_x/L

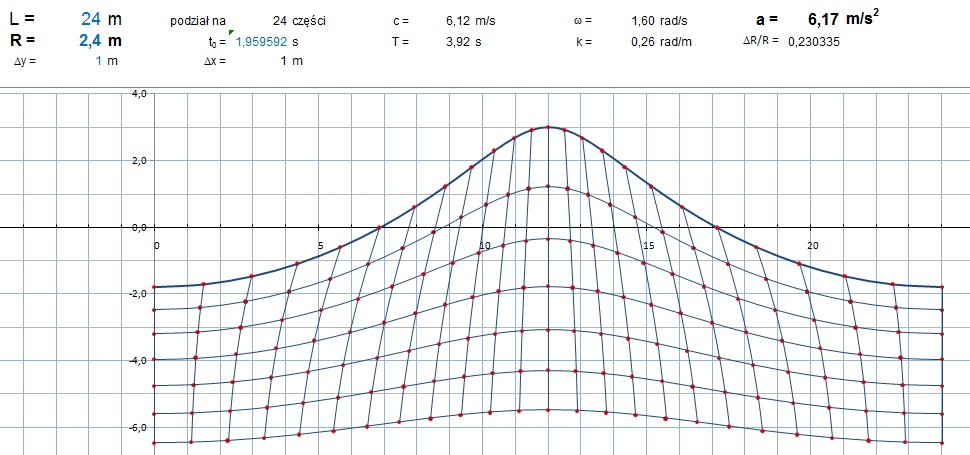
Rys. 8 Konstrukcja fali H/L = 0,2(A_z/L=0,1) z cyrkulacją eliptyczną i podniesieniem środków cyrkulacji o πA_zA_x/L

Zwróćmy uwagę, że różnica pomiędzy falami łagodnymi H/L=0,1 na rys. 5 i 7 jest minimalna. Natomiast dwa razy wyższe fale o H/L=0,2 na rys. 6 i 8 różnią się nieco bardziej kształtem. Szczyt fali jest łagodniejszy, szerszy. Pola elementów siatki różnią się od początkowych: w przypadku fali z rys. 8 (H/L=0,2) - do 3,2%; w przypadku fali z rys. 7 (H/L=0,1) - do 0,8%. Jesteśmy więc prawie o rząd bliżej spełnienia warunku nieściśliwości i zachowania masy ośrodka. Jeśli powiększylibyśmy fale do H/L=0,3 (rys. 9) opis ruchu eliptycznego daje błąd objętości elementu do 11,8% a wcześniejsze przybliżenie kołowe 57% i nierealny kształt fali. Zwróćmy uwagę, że błąd 57% in minus oznacza, że błąd przewyższa wartość. To właściwie dyskwalifikuje hipotezę ruchu po okręgu dla stromych fal gdzie rotacja odbywa się z przyspieszeniem dośrodkowym bliskim g. Oczywiście pamiętajmy, ze takie fale w realnych warunkach mogą wcale nie powstawać z zupełnie innych powodów.

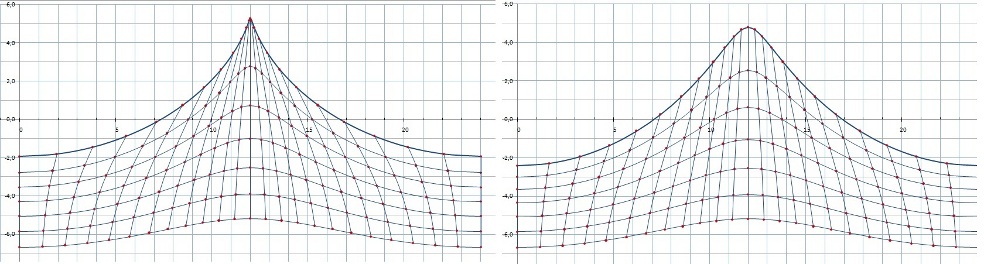
Rys.9 Kształt fali dla H/L = 0,3. Z lewej - konstrukcja oparta na cyrkulacji kołowej, z prawej – na eliptycznej.

Oto zestawienie maksymalnych rozbieżności pól elementów dla obu modeli przy rozmiarach elementu Δx = Δz = L/24:

Trajektoria ruchu	H/L=0,1	H/L=0,2	H/L=0,3
Okrąg	8,7%	20,8%	57%
Elipsa	0,8%	3,2%	11,8%

Wartości te mogą zależeć również od wielkości elementu siatki, ale jak widać główne rozbieżności wynikają z modelu ruchu, a nie z metody czy dokładności obliczeń.

Ruch po elipsie charakteryzują dwie wielkości geometryczne: amplituda pionowa A_z i amplituda pozioma A_x , a nie tak jak w ruchu po okręgu jedna wielkość – promień R. Będziemy musieli zmienić nawyki i uznać, że wysokość fali H = 2A_z . Konstrukcja fal dla cyrkulacji eliptycznych bazuje na dwóch dodatkowych zależnościach stanowiących istotę:

amplitud ruchów poziomych i pionowych
$A_x=\Big(1-\frac{H}{L}\Big)A_z=\Big(1-\frac{2A_z}{L}\Big)A_z$ lub inaczej $\frac{A_z-A_x}{A_z}= \frac{H}{L}= \frac{2A_z}{L}$ (15)
podniesienia środków cyrkulacji:
$\Delta Z=\frac{\pi A_z A_x}{L}= \frac{\pi}{L}A_z A_x$ albo $\Delta Z L=\pi A_z A_x$ (16)

Zwróćmy uwagę, że zależność (15) mówi, że względna różnica amplitud pionowej i poziomej jest równa stromości fali H/L, a zależność (16) wyraża równość pól „niedoboru wody” i pola elipsy cyrkulacji.

Mając na uwadze, że wielkości A_z, A_x, H, ΔZ są właściwie zmiennymi A_z(z) i A_x(z), H(z), ΔZ(z) zależnymi od głębokości z - można zapisać:

$A_x(z)= \Big(1-\frac{H(z)}{L}\Big)A_z(z)= \Big(1-\frac{2 A_z(z)}{L}\Big)A_z(z)$ (15a)

$\Delta Z(z)= \frac{\pi}{L}A_x(z)A_z(z)= \frac{\pi}{L}\Big(1-\frac{2 A_z(z)}{L}\Big)A_z(z)^2$ (16a)

Oczywiście znalezione zależności mają jedynie siłę hipotezy, nie dowodu i są przybliżeniem rzeczywistości, ale przybliżeniem nie prowadzącym do absurdalnych kształtów fal i poprawiającym dokładność w zakresie stromych fal prawie o rząd. Mnie to satysfakcjonuje.

Równania falowe ruchu cząstek wody o współrzędnych początkowych x, z przyjmą postać podobną do równań (13):

$\left\{\begin{array}{ll}X=x+A_x(z)\cos(kx-\omega t)\\Z=z+\Delta Z(z)+ A_z(z)\sin(kx-\omega t)\end{array}\right.$ (17)

Gdzie:

$A_z(z)= \frac{H}{2}e^{kz}$ ; $A_x(z)= \Big(1-\frac{2A_z(z)}{L}\Big)A_z(z)$ ; $\Delta Z=\frac{\pi}{L}A_x(z)A_z(z)$ (18)

Po wstawieniu wzorów (18) do (17) otrzymamy:

$\left\{\begin{array}{ll}X=x+\frac{H}{2}e^{kz}\Big(1-\frac{H}{L}e^{kz}\Big)\cos(kx-\omega t)\\Z=z+\frac{H}{2}e^{kz}\bigg(\frac{\pi}{2}\Big(1-\frac{H}{L}e^{kz}\Big)\frac{H}{L}e^{kz}+ \sin(kx-\omega t)\bigg)\\\end{array}\right.$ (19)

Gdybyście chcieli sami stworzyć, arkusz, program, animację - macie gotowe wzory, ale i tak prościej wyliczyć najpierw dla każdego z wielkości ze wzorów (18), a potem wstawić do (17).

Te dociekania pozwalają powiedzieć coś o zakresie stosowalności modelu opartego na cyrkulacjach kolistych. Ważne wnioski są następujące:

W falach o amplitudzie małej w porównaniu z ich długością ruch cząstek odbywa się po okręgu.
W falach o znacznej, w porównaniu z długością, amplitudzie ruch po okręgu jest jedynie przybliżeniem. Znacznie lepszym opisem jest ruch eliptyczny.
Składowa pionowa przyspieszenia cząstek wody zależy jedynie od stosunku amplitudy ruchów pionowych do długości fali lub inaczej od stromości fali.
Dywagacje dotyczące ciążenia i wyporu w szczycie i dolinie fali oparte na kinematyce ruchu po okręgu – można uznać za dość dokładne, zaś dotyczące kształtu fal, kierunku wypadkowych sił (przyspieszeń) poziomych skośnych – nie bardzo.

Analogia do wahadła matematycznego

Wahadło matematyczne to punkt materialny o masie m na nieważkim ramieniu o długości l. Wzór na okres drgań wahadła matematycznego, wyprowadzony przy założeniu małych wychyleń w stosunku do długości wahadła, wygląda następująco:

$T=2\pi\sqrt{\frac{l}{g}}$ (20)

Zapiszmy zależność okresu fal od ich długości, wykorzystując związek dyspersyjny wyprowadzony również dla małych amplitud fal:

$T_w=\frac{L}{c}= \frac{L}{\sqrt{\frac{g}{k}}}= L\sqrt{\frac{k}{g}}= L\sqrt{\frac{2\pi}{Lg}}= \sqrt{2\pi}\sqrt{\frac{L^2}{Lg}}= \sqrt{2\pi}\sqrt{\frac{L}{g}}$ (21)

Bardzo podobne prawda? Wahadło i fala oscylują pod wpływem grawitacji. W obu przypadkach, dla małych w stosunku do długości amplitud, rozwiązania dynamiczne dają oscylacje harmoniczne wokół punktów równowagi o okresie niezależnym od masy (gęstości), proporcjonalnym do pierwiastka z długości i odwrotnie proporcjonalnym do pierwiastka z przyspieszenia ziemskiego.

Zauważmy, że fala o długości równej obwodowi okręgu, jaki zatoczyłoby wahadło wykonując pełny obrót, czyli L=2πl, ma okres drgań równy okresowi wahadła matematycznego:

$T_w=\sqrt{2\pi}\sqrt{\frac{L}{g}}= \sqrt{2\pi}\sqrt{\frac{2\pi l}{g}}= \big(\sqrt{2\pi}\big)^2\sqrt{\frac{l}{g}}= 2\pi\sqrt{\frac{l}{g}}$ (22)

Niezwykle elegancka zależność!

Czy analogia ta ma głębsze konsekwencje? W szczególności, czy okres fal stromych jest dłuższy niż łagodnych tej samej długości, tak jak okres dużych drgań wahadła? Jeśli tak to również prędkość rozchodzenia się fal stromych może być różna od tej określonej związkiem dyspersyjnym. Co zatem z interferencją fal o nieznacznie różniących się prędkościach i tych samych długościach lub odwrotnie? Czy kiedy zaczęłyby interferować w zgodnej fazie wytwarzając wyższą falę, zmieniłyby nieznacznie prędkość i od tej pory zostały złączone we wspólnym biegu? Czy to mógłby być jeden z mechanizmów wzrastania fal, agregowania ich i tworzenia się głównego ciągu falowego. Czy mógłby to być mechanizm budowania się fal „dzikich”? Sporo pytań i temat do rozmyślań na później. Nie znam na nie odpowiedzi.

Na koniec pragnę przyznać, że tytuł „Anatomia fal” zaczerpnąłem ze wspomnianego dzieła Czesława Marchaja, które bardzo cenię. To tytuł jednego z rozdziałów – lapidarny w formie – dotykający najistotniejszego aspektu. Właśnie kształt fal jest najważniejszą manifestacją specyficznej kinematyki ich ruchu. Właśnie ta „anatomia” każe dostrzec w falach grawitacyjnych na granicy ośrodków płynnych zjawisko, choć podobne do innych prostych modeli fal, to jednak istotnie różne. Właśnie ta budowa fal prowadzi do ważkich wniosków dotyczących dynamiki ruchu fal i ciał biorących udział w tym ruchu – łodzi, jachtów, statków.

Jacek Pasikowski